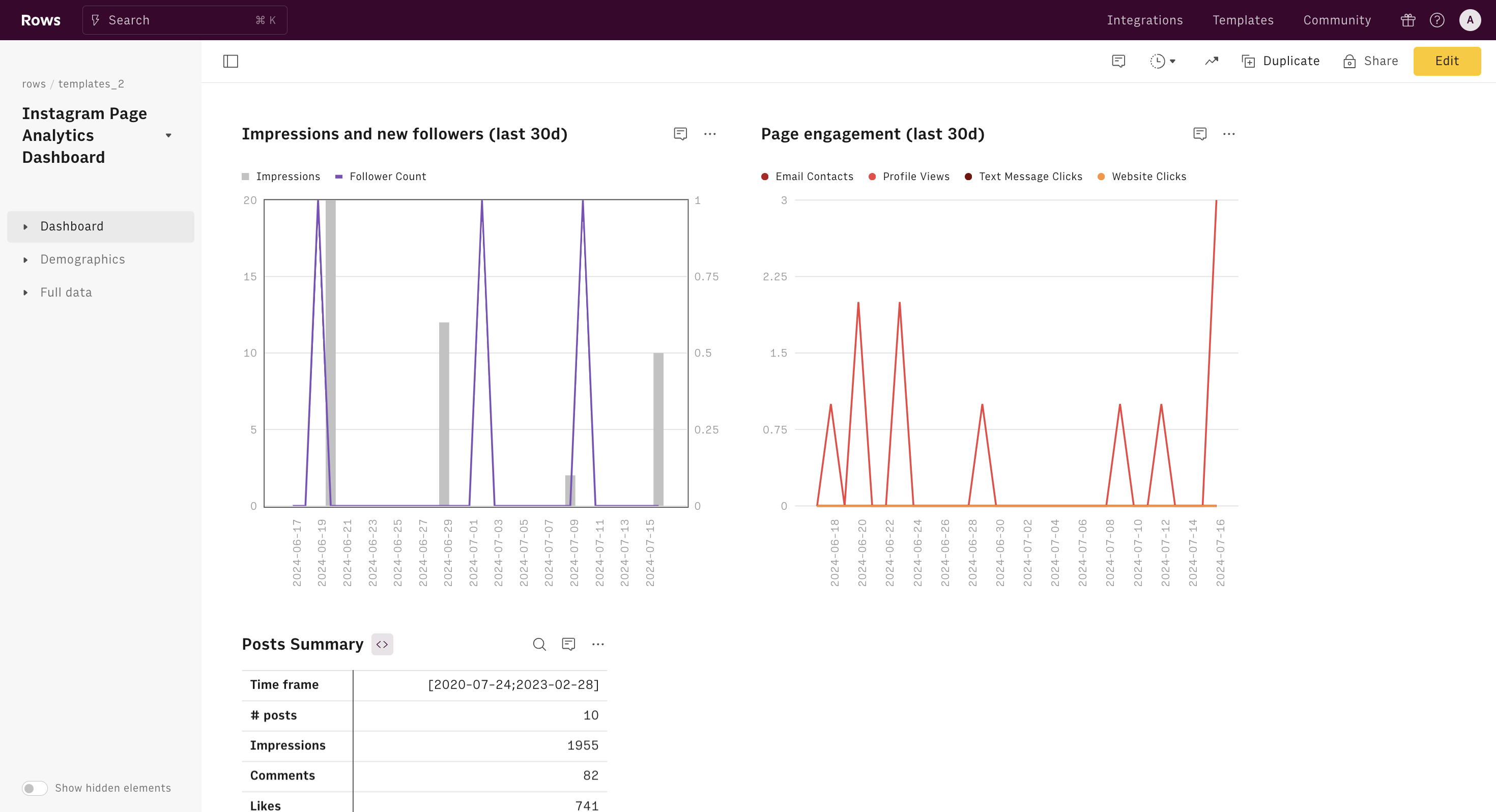
The Bond Pricing calculator helps you calculate the price of a bond, given its coupon, face value, maturity, and prevalent discount rate on the market.
A bond is a financial instrument representing a debt obligation. It is a loan made by investors to governments, municipalities or corporations, with the borrower promising to repay the borrowed amount (face value) on a specified future date (maturity). Interest payments (coupon) are made to bondholders during the bond's lifetime. Bonds are used to raise capital and provide investors with fixed income.
Required input:
Coupon value, namely the value of the periodic interest payments made by the issuer of the bond to the bondholders as compensation for lending their money to the issuer. It is often expressed as a percentage of the bond's face value, the coupon rate
Face value, namely the amount borrowed by the issuer. Bonds can be issued "at par", "sub-par" or "above par", depending on their issuance price. Issuance "at par" refers to the situation where the bonds are sold to investors at their face value. "Sub-par" bond issuance occurs when the bonds are sold to investors at a price below their face value. This means that investors are purchasing the bonds at a discount, paying less than its nominal value, thus enabling the investor to benefit from an additional capital gain when held to maturity. The discount may be a result of various factors, such as market conditions, credit risk, or changes in interest rates. FInally, "above par" issuance refers to selling bonds at a price higher than their face value. In this case, investors are purchasing the bonds at a premium, paying more than the bond's nominal value. Usually happens when demand is extremely high and investors are willing to give up some of the overall in exchange for extra safety.
Maturity, namely the time at which the principal of the bond, its face value, is paid back to the investor.
Discount rate, is the rate used to discount all the future cash flows and determine their Present Value, i.e. the price at which the bond trades. It represents the opportunity cost of money, i.e. having to wait for future payment and not being able to invest at the prevailing market rate. The discount rate used is the yield to maturity, which is the rate of return that an investor will get if they reinvested every coupon payment from the bond at a fixed interest rate until the bond matures
The bond price is calculated as follows:
Price = Coupon value*[(1-(1+Discount Rate)^(-Maturity)]/Discount rate)+Face value/(1+Discount rate)^Maturity
Practical example:
|
|
|---|---|
Coupon value | $ 50 |
Discount rate | 2.75% |
Bond face value | $ 1,000 |
Years to maturity | 10 |
The price is $1,194. This bond trades above par as the prevailing interest rate in the market (2,75%) is lower than its coupon rate (50$ / 1000$ = 5%): this means that - if someone wants to buy it - she needs to pay a premium to compensate the current holder.
A variation of regular bonds, often issued by governments, is the zero-coupon bond, a type of security that does not pay regular interest payments. Instead, these bonds are initially sold at a discounted price relative to their face value and provide a lump sum payment to the bondholder at maturity. The difference between the discounted purchase price and the face value represents the bond's return, which is earned over the holding period.
When analyzing bond prices, financial analysts investigate the following variables:
Current Interest Rates: The prevailing interest rates in the market have a significant impact on bond prices. When market interest rates rise, the prices of existing bonds with lower coupon rates become less desirable, resulting in a decrease in their prices. Conversely, when market interest rates decline, bond prices tend to rise.
Duration: it's a measure of the bond's sensitivity to changes in interest rates, and it is affected by factors such as the bond's maturity, coupon rate, and yield. Longer-duration bonds are typically more sensitive to interest rate changes and therefore have higher price volatility than shorter-duration bonds. As a result, investors often demand a higher yield on longer-duration bonds to compensate for this added risk. Conversely, shorter-duration bonds are typically less sensitive to interest rate changes and therefore have lower price volatility, which makes them less risky and generally more expensive.
Maturity: The time remaining until a bond matures also influences its price. Generally, longer-term bonds have more price volatility in response to changes in interest rates compared to shorter-term bonds. As a result, longer-term bonds typically have higher yields and, therefore, lower prices compared to bonds with shorter maturities.
Market Supply and Demand: The overall demand for and supply of bonds in the market can impact their prices. If there is strong demand for a particular bond, its price may rise. Conversely, if there is limited demand or an oversupply of bonds, prices may decline.
Call Provision: Some bonds include a call provision that allows the issuer to redeem or "call" the bonds before their maturity date. The presence of a call provision can affect bond prices, as investors may anticipate the possibility of early redemption and adjust their pricing accordingly.
Credit Rating: The creditworthiness of the bond issuer, as determined by credit rating agencies, affects bond prices. Bonds issued by entities with higher credit ratings - such as solid businesses or trustworthy governments - are considered less risky and, therefore, tend to have higher prices. In contrast, bonds with lower credit ratings or those considered higher risk will generally have lower prices to compensate for the added risk.
The credit rating assessment is particularly relevant when dealing with government-issued bonds: the Argentine Bond Crisis of 2001 is a noteworthy example, when a severe economic and financial crisis was triggered by the default on its $132 billion sovereign debt, due to its inability to meet its debt obligations. When investors lose confidence in the country's ability to repay its debts, they start selling them highly sub-par, and prices plummet. When those bonds belong to the asset side of financial institutions' balance sheets, the need "to mark to market" determines huge losses that propagate through the bank depositors and the economy as a whole.