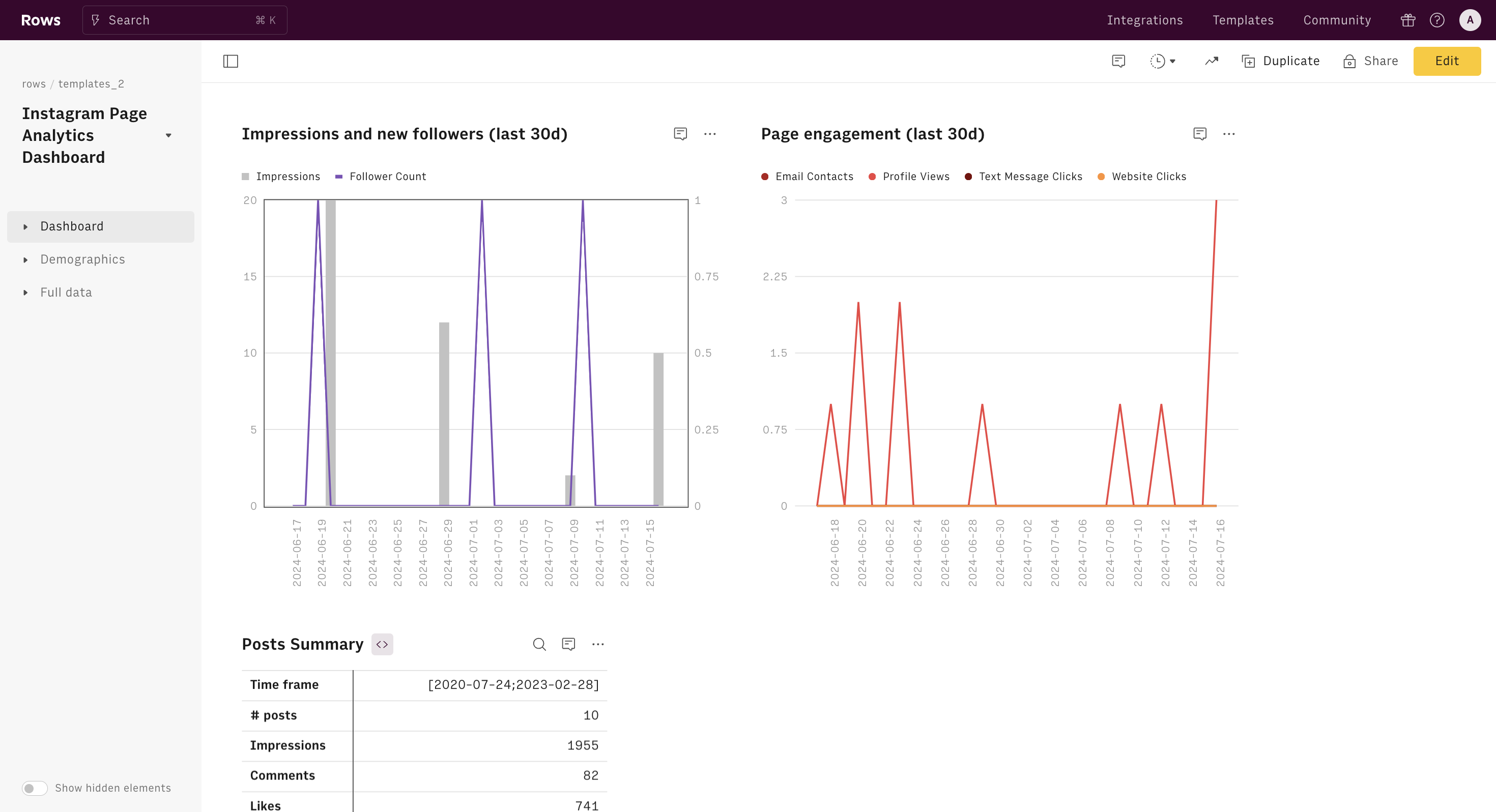
What is a Quadratic Formula Calculator?
A quadratic equation is a type of polynomial equation that takes the form ax² + bx + c = 0, where a, b, and c are numbers. The Quadratic Equation Formula is derived from the process of completing the square and provides a straightforward way to calculate the roots of any quadratic equation.
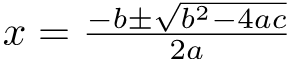
This allows you to determine the values of x that satisfy the equation, offering both real and complex solutions depending on the discriminant.
How to use the Quadratic Formula Calculator
Using our calculator is simple and. Follow these steps to get your results:
Identify the Coefficients: Locate the values of a, b, and c in your quadratic equation written in the standard form ax² + bx + c = 0.
Enter the Values: Input the coefficients into the designated fields in the calculator:
a: Coefficient of x²
b: Coefficient of x
c: Constant term
View Results: The calculator will apply the quadratic formula and display the solutions for x, including real roots. For equations with complex roots, it will indicate that no real solutions exist.
Example of Quadratic Equations
Let's take the following example: x² + 5x + 6 = 0
First, calculate the discriminant (Δ)= b²-4*a*c :
Δ = 5² - 4(1)(6) = 25 - 24 = 1
Next, apply the quadratic formula:
x = (-5 ± √1) / 2
Simplify the expression:
x = (-5 ± 1) / 2
Calculate the two possible solutions:
x = (-5 + 1) / 2 = -4 / 2 = -2
x = (-5 - 1) / 2 = -6 / 2 = -3
Solutions: x = -2 and x = -3
FAQ
What is meant by the quadratic equation?
A quadratic equation is a second-order polynomial equation in a single variable x, with the form ax² + bx + c = 0, where a, b, and c are constants. The solutions to this equation are the values of x that make the equation true.
What is discriminant?
The discriminant of a quadratic equation is the part of the quadratic formula under the square root, b² - 4ac. It determines the nature of the roots:
If the discriminant is positive, there are two distinct real roots.
If the discriminant is zero, there is one repeated real root.
If the discriminant is negative, there are two complex roots.
What is the standard form of the quadratic equation?
The standard form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and x represents the variable. This form allows the use of the quadratic formula to find the roots.
What are the four different methods to solve the quadratic equation?
There are four primary methods to solve a quadratic equation:
Factoring: Expressing the quadratic equation as a product of two binomials.
Quadratic Formula: Using the formula x=2a−b±b2−4ac to find the roots.
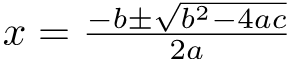
Completing the Square: Rewriting the equation in the form (x+p)2=q.
(x+p)2=q(x + p)² = q
Graphing: Plotting the quadratic equation and finding the points where it intersects the x-axis.